Revolutionizing Data Insights: How Google DeepMind is Redefining Regression with Decoding Techniques

Regression responsibilities, which entail forecasting continuous numerical values, have conventionally depended on numerical outputs such as Gaussian parameterizations or pointwise tensor projections. These conventional methodologies impose significant distributional assumption requirements, necessitate extensive labeled data, and often falter when modeling sophisticated numerical distributions. Recent advancements in large language models present an alternative method—representing numerical values as sequences of discrete tokens and utilizing auto-regressive decoding for forecasting. Nevertheless, this transition is accompanied by several formidable challenges, including the necessity for an efficient tokenization process, the risk of numeric precision loss, the imperative to sustain stable training, and the requirement to address the absence of inductive bias in sequential token formats for numeric values. Surmounting these obstacles could result in a more powerful, data-efficient, and adaptable regression framework, thereby broadening the application of deep learning models beyond conventional techniques.

Conventional regression models depend on numerical tensor projections or parametric distribution heads, such as Gaussian models. While these traditional strategies are well-established, they possess multiple limitations. Gaussian-based models are constrained by the assumption of normally distributed outputs, limiting their capability to model more sophisticated, multimodal distributions. Pointwise regression heads encounter difficulties with highly non-linear or discontinuous relationships, restricting their generalization capacity across diverse datasets. High-dimensional models, like histogram-based Riemann distributions, are both computationally and data-intensive, rendering them inefficient. Additionally, many traditional techniques demand explicit normalization or scaling of outputs, introducing an extra layer of complexity and potential instability. While conventional studies have attempted to utilize text-to-text regression with large language models, minimal systematic exploration has been conducted on “anything-to-text” regression, where numerical outputs are formulated as sequences of tokens, thereby unveiling a new paradigm for numeric forecasting.

Researchers affiliated with Google DeepMind propose an alternative formulation for regression, rearticulating numeric prediction as a problem of auto-regressive sequence generation. Instead of producing scalar values directly, this technique encodes numbers as token sequences and utilizes constrained decoding to generate valid numerical outputs. Encoding numerical values as sequences of discrete tokens enhances flexibility and expressiveness when modeling real-valued data. Unlike Gaussian-based strategies, this approach does not impose rigorous distributional assumptions about the data, thereby enhancing its generalizability to real-world tasks characterized by diverse patterns. The model enables precise modeling of multimodal, complex distributions, consequently enhancing its efficacy in density estimation as well as pointwise regression endeavors. By capitalizing on the benefits of autoregressive decoders, it harnesses recent advancements in language modeling while maintaining competitive performance against standard numerical heads. This formulation provides a resilient and adaptable framework capable of precisely modeling a broad spectrum of numeric relationships, presenting a practical alternative to conventional regression techniques typically seen asinflexible.

Transforming Numeric Prediction with Google DeepMind’s Tokenization Strategy

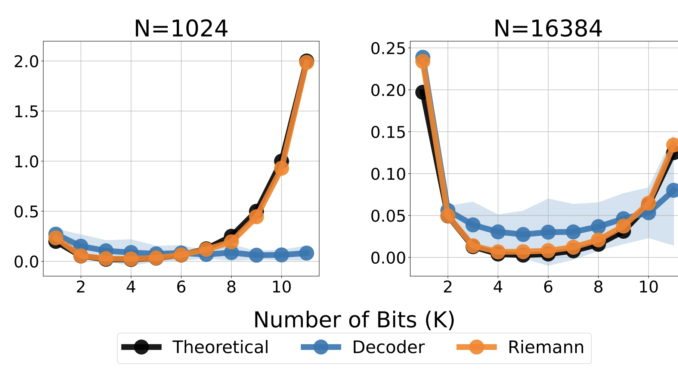
This methodology utilizes two tokenization strategies for numeric representation: normalized tokenization and unnormalized tokenization. Normalized tokenization encodes numbers within a fixed range using base-B expansion to provide finer precision with increasing sequence lengths. Unnormalized tokenization extends the same concept to broader numeric ranges through a generalized floating-point representation, such as IEEE-754, without necessitating explicit normalization. An auto-regressive transformer model generates numerical outputs token by token, adhering to constraints to produce valid numeric sequences. The model is trained using cross-entropy loss across the token sequence to ensure accurate numeric representation. Instead of directly forecasting a scalar output, the system samples token sequences and applies statistical estimation methodologies, such as mean or median calculations, for the final prediction. Evaluations are performed on authentic tabular regression datasets from OpenML-CTR23 and AMLB benchmarks, comparing it against Gaussian mixture models, histogram-based regression, and conventional pointwise regression heads. Hyperparameter optimization is carried out over various decoder configurations, including variations in the number of layers, hidden units, and token vocabularies, to achieve enhanced performance.

Experiments demonstrate that the model adeptly captures intricate numeric relationships, achieving impressive performance across a variety of regression tasks. It achieves elevated Kendall-Tau correlation scores on tabular regression, frequently surpassing baseline models, particularly in low-data environments where numeric stability is critical. The approach also excels in density estimation, effectively capturing complex distributions and ranking better than Gaussian mixture models and Riemann-based methods in negative log-likelihood assessments. Optimizing model size from the outset enhances performance, with excessive capacity leading to overfitting. Numeric stability is significantly improved through error correction techniques, including token repetition and majority voting, reducing vulnerability to outliers. These findings highlight this regression framework as a robust and adaptive alternative to traditional methods, demonstrating its capability to generalize effectively across various datasets and modeling challenges.

This research presents an innovative method for numeric forecasting by utilizing tokenized representations and auto-regressive decoding. By replacing conventional numeric

By utilizing regression heads with token-oriented outputs, the framework enhances adaptability in modeling continuous data. It achieves impressive results across various regression challenges, particularly in density assessment and tabular data analysis, while also offering theoretical assurances for approximating any arbitrary probability distributions. It surpasses conventional regression techniques in critical scenarios, notably in handling complex distributions and limited training instances. Prospective efforts will focus on refining tokenization methods for improved numeric accuracy and reliability, broadening the framework to encompass multi-output regression and high-dimensional prediction challenges, and exploring its use in reinforcement learning reward modeling and vision-driven numeric estimation. These findings render sequence-based numeric regression a compelling substitute for traditional approaches, broadening the range of tasks that language models can efficiently address.

Explore the Paper and GitHub Page. All recognition for this investigation goes to the project’s researchers. Additionally, don’t forget to follow us on Twitter, and join our Telegram Channel and LinkedIn Group. Also, feel free to join our 75k+ ML SubReddit.

🚨 Marktechpost is inviting AI Companies/Startups/Groups to collaborate for its forthcoming AI Magazines on ‘Open Source AI in Production’ and ‘Agentic AI’.